1. Bildungsauftrag des Faches Mathematik

„Mathematik durchzieht eine Vielzahl von Bereichen des täglichen Lebens. Vielfach erlauben erst Vorstellungen von räumlichen Beziehungen und geometrischen Darstellungsweisen den Zugang zu Problemstellungen. Zahlen, Berechnungen und graphische Darstellungen prägen Ergebnisse angewandter mathematischer Methoden und beschreiben Zusammenhänge. Mathematische Begriffe und Methoden bilden somit die Grundlage weitreichender Entscheidungen bei unterschiedlichen Vorgängen in der Gesellschaft. Damit leistet der Mathematikunterricht in zeitgemäßer Weise einen Beitrag zur Allgemeinbildung der Schülerinnen und Schüler.

Mathematik beschränkt sich nicht auf einen abgeschlossenen Wissenskanon, sondern steht vielmehr für lebendiges und phantasievolles Handeln, das auf menschlicher Kreativität beruht. Schülerinnen und Schüler erfahren Mathematik als ein Werkzeug zur Beschreibung und Bearbeitung von Aufgaben und Problemen inner- und außerhalb der Mathematik. Anregung zur Eigentätigkeit, Einlassen auf die Vorerfahrungen der Lernenden und das Vernetzen von Kenntnissen fördern die geistige Aktivität und erhöhen die Chancen für das Verstehen.

Mathematikunterricht fördert grundlegende intellektuelle Fähigkeiten, die über das Fach hinaus von Bedeutung sind, wie z. B. Ordnen, folgerichtiges Denken, Verallgemeinern und Abstrahieren. Daneben fördert mathematisches Handeln durch Erkunden von Zusammenhängen, Argumentieren, Systematisieren, Entwickeln und Untersuchen von Strukturen die allgemeine Handlungskompetenz. Die Schülerinnen und Schüler erschließen sich einen Wahrnehmungs- und Urteilshorizont, der über die Alltagsvorstellungen hinausgeht und die Kritikfähigkeit und Beurteilungskompetenz fördert.“ (siehe KC Mathematik der IGS)

Ein Mathematikunterricht, der die subjektiven Sichtweisen der Schülerinnen und Schüler ernst nimmt, bietet Gelegenheiten für Umwege, alternative Deutungen und Ideenaustausch und legt Wert auf eigenverantwortliches Handeln. Komplexe mathematische Fragestellungen und Probleme werden bearbeitet, indem die Schülerinnen und Schüler auch miteinander kommunizieren und kooperieren. Auf diese Weise erfahren die Schülerinnen und Schüler die Bedeutung ihres mathematischen Handelns, entwickeln Selbstvertrauen in die eigenen mathematischen Kompetenzen sowie Phantasie, Kreativität, Interesse und Neugier an mathematikhaltigen Phänomenen.

 

2. Kompetenzorientierter Mathematikunterricht

Der Aufbau der erforderlichen inhaltsbezogenen und prozessbezogenen Kompetenzen ist neben grundlegenden intellektuellen Zielen verbunden mit allgemein bildenden und übergreifenden Zielen zur Persönlichkeitsentwicklung sowie zur Förderung des eigenen und des sozialen Lernens zur Erreichung einer allgemeinen Handlungskompetenz.

Sowohl die prozess- als auch inhaltsbezogenen Kompetenzbereiche finden Eingang in jede Unterrichtsstunde, jedes Feedback und jeden Lernentwicklungsbericht.

Prozessbezogene Kompetenzbereiche:

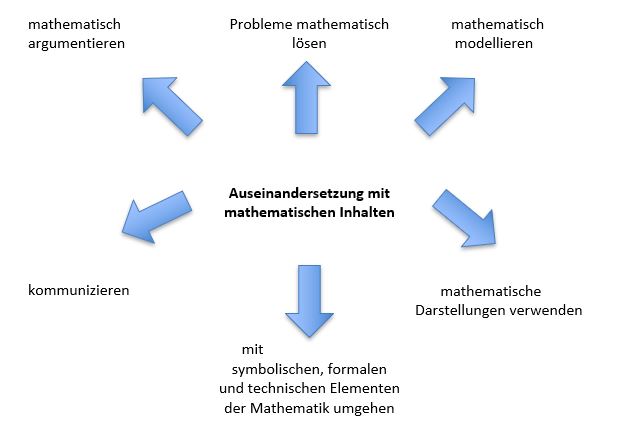
Die prozessbezogenen Kompetenzbereiche stimmen in allen Jahrgängen überein. Die inhaltsbezogenen Kompetenzbereiche der Sekundarstufe I umfassen "Zahlen und Operationen", "Größen und Messen", "Raum und Form", "Funktionaler Zusammenhang" und "Daten und Zufall". 
In der gymnasialen Oberstufe werden die Inhalte um "Algorithmus", "Räumliches Strukturieren und Koordinatisieren" erweitert; hier werden die Inhalte den Sachgebieten Analysis, Stochastik, Lineare Algebra und Analytische Geometrie zugeordnet.

Inhaltsbezogene Kompetenzbereiche der Sekundarstufe I:

Zahlen und Operationen

Zahlen sind Bestandteil des täglichen Lebens. Sie dienen dazu, Phänomene aus der Umwelt zu quantifizieren und zu vergleichen. Schülerinnen und Schüler entwickeln ein grundlegendes Verständnis von Zahlen, Variablen, Rechenoperationen, Umkehrungen, Termen und Formeln. Sie wählen, beschreiben und bewerten Vorgehensweisen und Verfahren, denen Algorithmen bzw. Kalküle zu Grunde liegen.

Größen und Messen

Zählen und Messen dienen dazu, Phänomene aus der Umwelt zu quantifizieren und zu vergleichen.

Schülerinnen und Schüler entwickeln ein grundlegendes Verständnis vom Prinzip des Messens. Sie wenden dieses zur Orientierung, zur Durchdringung lebensweltlicher Probleme und zur Begründung von Formeln an.

Raum und Form

Die Untersuchung geometrischer Objekte und der Beziehungen zwischen ihnen dient der Orientierung im Raum und ist Grundlage für Konstruktionen, Berechnungen und Begründungen. Bei der Beschäftigung mit Geometrie spielen ästhetische Aspekte eine besondere Rolle. Die Schülerinnen und Schüler entwickeln ihr räumliches Vorstellungsvermögen weiter. Hierbei steht der handelnde und ästhetische Aspekt vor dem rechnerischen Lösen von Aufgaben. Zum Erwerb geometrischer Kompetenzen ist ein ständiger Wechsel zwischen dem Herstellen, dem Beschreiben, dem Darstellen und dem Berechnen geometrischer Objekte wichtig.

Funktionaler Zusammenhang

Funktionen sind ein zentrales Mittel zur mathematischen Beschreibung quantitativer Zusammenhänge. Mit ihnen lassen sich Phänomene der Abhängigkeit und der Veränderung von Größen erfassen und analysieren. Funktionen eignen sich für Modellierungen für eine Vielzahl von Realsituationen. Schülerinnen und Schüler entwickeln ein grundlegendes Verständnis von funktionalen Abhängigkeiten.

Daten und Zufall

Die Analyse und Bewertung von Datenmaterial bietet die Grundlage für Entscheidungen sowie für die Abschätzung von Chancen und Risiken. Wahrscheinlichkeiten dienen der Beschreibung von Zufallsphänomenen und ermöglichen Prognosen. Schülerinnen und Schüler entwickeln ein grundlegendes Verständnis von Prognosen und Simulationen.

Die fünf inhaltsbezogenen Kompetenzen werden in den folgenden Lernbereichen neu strukturiert und stärker thematisch gegliedert.

Der Lernbereich

• Umgang mit Zahlen … umfasst alle Zahlenbereichsentwicklungen sowie die Behandlung von Variablen und Termdarstellungen,

• Umgang mit Veränderungen  … stellt die systematische Entwicklung eines  Funktionsbegriffs in den Mittelpunkt,

• Umgang mit Daten und Wahrscheinlichkeiten … enthält alle stochastischen und statistischen Kompetenzen,

• Umgang mit Figuren und Körpern … behandelt die euklidische Geometrie, präzisiert geometrische   Begriffsbildungen und zielt auf die Entwicklung des räumlichen Vorstellungsvermögens ab.

 

3. Differenzierung im Mathematikunterricht

Das Fach Mathematik wird bis zum Ende des achten Jahrgangs binnendifferenziert unterrichtet.  Ab der 7. Klasse erhalten die Schülerinnen und Schüler zum Ende des Halbjahres eine Niveaustufeneinordnung, auf der sie im folgenden Halbjahr beurteilt werden. Sie können diese bestätigen oder auch in Frage stellen. In den Klassen 7 + 8 können sie sich immer wieder auch größeren Herausforderungen stellen und das höhere Niveau wählen.

Ab der neunten Klasse erfolgt auf der Grundlage der bisher gezeigten Leistungen eine Zuweisung in die Fachleistungskurse mit grundlegenden Anforderungen (G-Kurs) und auf erhöhtem Anforderungsniveau (E-Kurs). Eine Umstufung ist jeweils zum Halbjahr möglich und wird durch die Klassenkonferenz vorgenommen.

 

4. Das Schulbuch im Mathematikunterricht

An der IGS Embsen arbeiten wir im Doppeljahrgang 5/6 mit dem Schulbuch Mathematik + aus dem Westermann-Verlag. Einem Schulbuch, dessen didaktisches Konzept auf aktuellen Forschungsergebnissen basiert und umfassende Unterstützung für einen modernen Mathematikunterricht bietet, der auch einer differenzierenden Unterrichtsgestaltung gerecht wird. So wird in jedem Kapitel zunächst einen Wissensstandabfrage vorgenommen, damit alle „abgeholt“ werden können. Anschließend geht es um den Kompetenzaufbau, der mit vielen differenzierten Übungsmaterialien erarbeitet wird, ebenso fordern vertiefende Aufgabe den Transfer und die Reflexion. Jeweils in einem Ausgangstest lassen sich die erworbenen Kompetenzen überprüfen.

Im anschließenden Doppeljahrgang 7/8 arbeiten wir im Unterricht mit den Lehrwerken „Schnittpunkt“ aus dem Klett-Verlag. In diesem wird nach einer Anfangsdiagnose auf zwei Niveaustufen differenziert, so gibt es einen Lernweg für schwächere und einen für stärkere Schüler.

In dem Doppeljahrgang 9/10 erarbeiten wir Inhalte mit der Lehrwerksreihe „Schlüssel zur Mathematik“, sie stützt unsere Differenzierung auf zwei Niveaustufen und ermöglicht auch den Schülern in einer Niveaustufe auf die Lerninhalte des jeweils anderen Niveaus zu schauen, dieses kann die  Durchlässigkeit zwischen den Kursen bzw. Niveaustufen erleichtern.

In der Oberstufe haben wir die Lehrwerksreihe „Elemente der Mathematik“ aus dem Westermann-Verlag eingeführt, die in der 12. und 13. dem erhöhten und grundlegenden Anforderungsniveau nachkommt.

Neben dem Schulbuch werden häufig weitere Materialien, z.B. Arbeitshefte, eingesetzt, die Anschaffung wird jedoch immer der Lerngruppe angepasst und findet Eingang in die aktuelle Anschaffungsliste zu Beginn des Schuljahres.

 

5. Was uns wichtig ist...

Der Känguru-Wettbewerb, den Schülerinnen und Schüler schon von der Grundschule her kennen, ist uns auch ein besonderes Anliegen. Im 6. Jahrgang nehmen alle Schülerinnen und Schüler teil, in den folgenden Jahrgängen steht es ihnen frei.  Die Teilnahme wird ihnen ermöglicht und von der Schule unterstützt.

Ein weiteres Anliegen ist es, die Schülerinnen und Schüler zu unterstützen, sie zu fördern und fordern, wo und wie wir es nur können. Bezüglich des Förderns können wir auf unsere Übungszeiten in der Lerngruppe und auf die bisherigen Extrazeiten verweisen. In diesen können die Schülerinnen und Schüler Inhalte auf- bzw. nacharbeiten und werden von einer Lehrkraft unterstützt. Dem Fordern kommen wir im Moment nur im Rahmen des Unterrichtens nach, daran arbeiten wir...

Der Taschenrechner (WTR) wird im Laufe des 2. Halbjahrs des 7. Schuljahrs angeschafft, in der Sek II wird dann auf den CAS-Rechner gewechselt. Die Fachkonferenz Mathematik hat sich dabei für die folgenden Modelle entschieden: TI-30XPlus-MP (Jahrgang 7-10) und TI-Nspire CX II-T CAS (ab Sek II). Voraussichtlich wird die Anschaffung des TI-Nspire CX II-T CAS schon für den Prüfungsjahrgang 23/24 im 9. Jahrgang erforderlich. Weitere Informationen folgen.